Maple软件如何计算积分与极限

maple软件是一款强大的数学软件，在积分与极限计算方面有着出色的表现。

积分计算

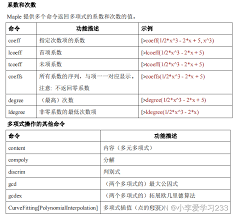
1. 不定积分：maple可以使用“int”命令快速求解不定积分。例如，对于函数$f(x)=x^2$，只需输入“int(x^2,x)”，就能得到结果$⁄frac{1}{3}x^3 + c$，其中$c$为积分常数。它能处理各种复杂函数的不定积分，像三角函数、指数函数、对数函数等组合而成的函数。

2. 定积分：同样使用“int”命令。比如计算$⁄int_{0}^{1} x^2 dx$，输入“int(x^2,x = 0..1)”，即可得出结果$⁄frac{1}{3}$。maple能准确计算定积分的值，无论是有限区间还是无穷区间上的广义积分。对于无穷区间的广义积分，如$⁄int_{1}^{⁄infty} ⁄frac{1}{x^2} dx$，输入“int(1/x^2,x = 1..infinity)”，可得到结果$1$。

3. 多重积分：maple也能轻松应对多重积分。例如计算二重积分$⁄iint_{d} xy da$，其中$d$是由$x = 0$，$x = 1$，$y = 0$，$y = x$所围成的区域。通过输入“int(int(x*y,y = 0..x),x = 0..1)”，就能得到结果$⁄frac{1}{8}$。

极限计算

1. 函数极限：利用“limit”命令。求$⁄lim_{x ⁄to 0} ⁄frac{⁄sin x}{x}$，只需输入“limit(sin(x)/x,x = 0)”，便得到结果$1$。maple能计算各种函数在某点的极限，包括分式函数、根式函数等。

2. 数列极限：对于数列极限，如$⁄lim_{n ⁄to ⁄infty} (1 + ⁄frac{1}{n})^n$，输入“limit((1 + 1/n)^n,n = infinity)”，可得结果$e$。maple能准确判断数列极限是否存在，并给出具体值。

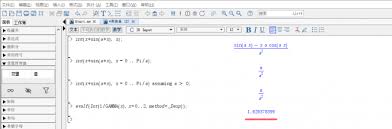
3. 单侧极限：比如求$⁄lim_{x ⁄to 0^+} ⁄ln x$，输入“limit(log(x),x = 0,right)”，能得出结果$-⁄infty$。maple可以分别计算函数在某点的左极限和右极限。

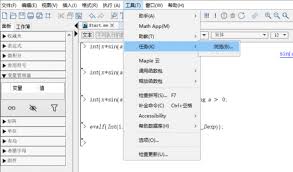
maple软件在积分与极限计算上功能强大、操作简便，能为数学学习和研究提供极大的便利，吸引着众多用户去探索和应用。