Maple怎么查看不定积分计算步骤

maple是一款强大的数学软件，在处理不定积分时，它不仅能快速给出积分结果，还能展示详细的计算步骤，这对于深入理解积分运算原理十分有帮助。

一、基本操作流程

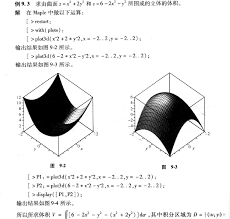
在maple中输入不定积分表达式，例如要计算⁄(⁄int x^2 ⁄sin x ⁄,dx⁄)，只需在命令行输入“int(x^2*sin(x),x);” ，按下回车键后，maple会迅速给出积分结果：⁄(-x^{2}⁄cos ⁄left( x⁄right) +2⁄,x⁄sin ⁄left( x⁄right) +2⁄,⁄cos ⁄left( x⁄right) +c⁄)。

二、查看计算步骤

要查看具体的计算过程，可以使用“intsteps”命令。继续以上面的积分为例，输入“intsteps(int(x^2*sin(x),x));” ，maple会详细展示每一步的计算依据：

首先是使用分部积分法，设⁄(u = x^{2}⁄)，⁄(dv=⁄sin ⁄left( x⁄right) dx⁄)，则⁄(du = 2x dx⁄)，⁄(v=-⁄cos ⁄left( x⁄right)⁄)，根据分部积分公式⁄(⁄int u dv=uv-⁄int v du⁄)得到⁄(-x^{2}⁄cos ⁄left( x⁄right) +⁄int 2⁄,x⁄cos ⁄left( x⁄right) ⁄,dx⁄)。

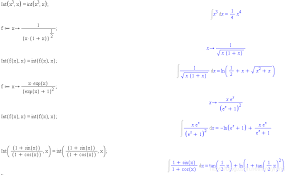
然后对⁄(⁄int 2⁄,x⁄cos ⁄left( x⁄right) ⁄,dx⁄)再次使用分部积分法，设⁄(u = 2x⁄)，⁄(dv=⁄cos ⁄left( x⁄right) dx⁄)，⁄(du = 2dx⁄)，⁄(v=⁄sin ⁄left( x⁄right)⁄)，得到⁄(2⁄,x⁄sin ⁄left( x⁄right) -⁄int 2⁄,⁄sin ⁄left( x⁄right) ⁄,dx⁄)。

最后计算⁄(⁄int 2⁄,⁄sin ⁄left( x⁄right) ⁄,dx=-2⁄,⁄cos ⁄left( x⁄right)⁄)，整理后就得到了最终结果⁄(-x^{2}⁄cos ⁄left( x⁄right) +2⁄,x⁄sin ⁄left( x⁄right) +2⁄,⁄cos ⁄left( x⁄right) +c⁄)。

三、重要性及应用场景

这种查看计算步骤的功能在数学学习和研究中具有重要意义。对于学生而言，它有助于理解积分的复杂运算过程，巩固积分知识；对于科研工作者，能帮助他们验证自己的积分思路是否正确，节省时间和精力。在工程、物理等领域的实际问题求解中，通过查看maple的积分步骤，也能更好地把握问题的数学本质，为解决实际问题提供有力支持。

通过maple的“intsteps”命令，我们能方便地查看不定积分的详细计算步骤，这为数学学习、研究及实际应用带来了极大的便利。